算法|最大堆、最小堆和堆排序的实现（JavaScript）

发表于 分类于 阅读次数： 本文字数： 1.7k 阅读时长 ≈ 6 分钟

讲解了数据结构中堆的一些概念以及实现，最后实现了一个堆排序算法。

一些概念

  • 堆：特殊的完全二叉树，具有特定性质的完全二叉树。
  • 大根堆：父节点 > 子节点
  • 小根堆：父节点 < 子节点

二叉堆也属于完全二叉树，所以可以用数组表示。

  • 若下标从1开始，左节点为 2*i ，右节点为 2*i+1 ，父节点为 i//2 。
  • 若下标从1开始，左节点为 2*i+1 ，右节点为 2*i+1+2 ，父节点为 (i-1)//2 。
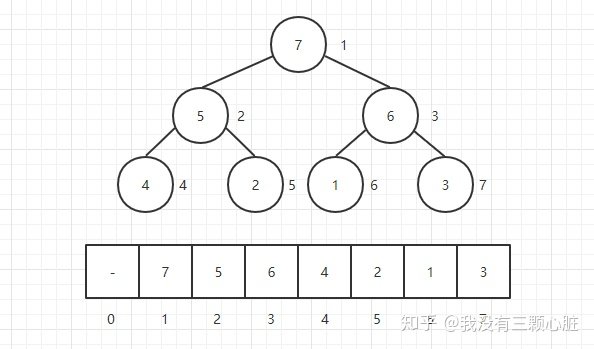
    image.png

最大堆

两个重要方法，插入元素和移出元素。

  • 插入元素：在堆尾插入元素，调用辅助方法，将该元素上浮到正确位置。
  • 移出元素：将堆尾元素删去并替换到堆首，将该元素下沉到正确位置。

解释：

  • 上浮：如果父节点更大，则替换，循环直至比父节点小。
  • 下沉：如果子节点中较大的那个更小，则替换，循环直至子节点都比自身小。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
class MaxHeap {
	constructor() {
		this.heap = []
	}
	isEmpty() {
		return this.heap.length === 0
	}
	size() {
		return this.heap.length
	}
	#getParentIndex(idx) {
		return Math.floor((idx-1)/2)
	}
	#getLeft(idx) {
		return idx * 2 + 1
	}
	#getRight(idx) {
		return idx * 2 + 2
	}
	// 插入
	insert(v) {
		this.heap.push(v)
		this.#swim(this.size()-1)
	}
	// 删除最大值
	deleteMax() {
		const max = this.heap[0]
		this.#swap(0, this.size() - 1) // 将根和最后一个元素交换
		this.heap.pop() // 防止对象游离
		this.#sink(0) // 下沉，恢复有序性
		return max
	}
	// 第i个是否小于第j个
	#compare(a, b) {
			return a < b
	}
	// 交换
	#swap(i, j) {
		[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]]
	}
	// 上浮
	#swim(k) {
		let parent = this.#getParentIndex(k)
		while(k > 0 && this.#compare(this.heap[parent], this.heap[k])) {
			this.#swap(parent, k)
			k = parent
			parent = this.#getParentIndex(k)
		}
	}
	// 下沉
	#sink(k) {
		while (this.#getLeft(k) < this.size()) {
			let j = this.#getLeft(k)
			// j 指向子节点的较大值
			if (j+1 < this.size() && this.#compare(this.heap[j], this.heap[j+1])) j++
			// 如果子节点都小
			if (this.#compare(this.heap[j], this.heap[k])) break
			this.#swap(k, j)
			k = j
		}
	}
}

测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const mh = new MaxHeap()
mh.insert(20)
mh.insert(80)
mh.insert(50)
mh.insert(40)
mh.insert(30)
mh.insert(40)
mh.insert(20)
mh.insert(10)
mh.insert(35)
mh.insert(15)
mh.insert(90)
console.log(mh.heap)
// [ <1 empty item>, 90, 80, 50, 35, 40, 40, 20, 10, 20, 15, 30 ]
mh.deleteMax()
mh.deleteMax()
mh.deleteMax()
console.log(mh.heap)
// [ <1 empty item>, 40, 35, 40, 20, 30, 15, 20, 10 ]

最小堆

与最小堆相比，仅是交换条件不同

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
class MinHeap {
	constructor() {
		this.heap = []
	}
	isEmpty() {
		return this.heap.length === 0
	}
	size() {
		return this.heap.length
	}
	#getParentIndex(idx) {
		return Math.floor((idx-1)/2)
	}
	#getLeft(idx) {
		return idx * 2 + 1
	}
	#getRight(idx) {
		return idx * 2 + 2
	}
	// 插入
	insert(v) {
		this.heap.push(v)
		this.#swim(this.size()-1)
	}
	// 删除最大值
	deleteMin() {
		const max = this.heap[0]
		this.#swap(0, this.size() - 1) // 将根和最后一个元素交换
		this.heap.pop() // 防止对象游离
		this.#sink(0) // 下沉，恢复有序性
		return max
	}
	// 第i个是否小于第j个
	#compare(a, b) {
			return a > b
	}
	// 交换
	#swap(i, j) {
		[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]]
	}
	// 上浮
	#swim(k) {
		let parent = this.#getParentIndex(k)
		while(k > 0 && this.#compare(this.heap[parent], this.heap[k])) {
			this.#swap(parent, k)
			k = parent
			parent = this.#getParentIndex(k)
		}
	}
	// 下沉
	#sink(k) {
		while (this.#getLeft(k) < this.size()) {
			let j = this.#getLeft(k)
			// j 指向子节点的较小值
			if (j+1 < this.size() && this.#compare(this.heap[j], this.heap[j+1])) j++
			// 如果子节点都大
			if (this.#compare(this.heap[j], this.heap[k])) break
			this.#swap(k, j)
			k = j
		}
	}
}

测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const mh = new MinHeap()
mh.insert(20)
mh.insert(80)
mh.insert(50)
mh.insert(40)
mh.insert(30)
mh.insert(40)
mh.insert(20)
mh.insert(10)
mh.insert(35)
mh.insert(15)
mh.insert(90)
console.log(mh.heap)
// [10, 15, 20, 30, 20, 50, 40, 80, 35, 40, 90]
mh.deleteMin()
mh.deleteMin()
mh.deleteMin()
console.log(mh.heap)
// [20, 30, 40, 35, 40, 50, 90, 80]

堆（自定义比较函数）

默认为最大堆，根据元素的大小进行排序，可自定义排序规则，返回值为布尔值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
class Heap {
	constructor(compareFn) {
		this.heap = []
		this.compare = (typeof compareFn === 'function') ? compareFn : this.#defaultCompare
	}
	isEmpty() {
		return this.heap.length === 0
	}
	size() {
		return this.heap.length
	}
	#getParentIndex(idx) {
		return Math.floor((idx-1)/2)
	}
	#getLeft(idx) {
		return idx * 2 + 1
	}
	#getRight(idx) {
		return idx * 2 + 2
	}
	// 插入
	insert(v) {
		this.heap.push(v)
		this.#swim(this.size()-1)
	}
	// 删除最大值
	delete() {
		const max = this.heap[0]
		this.#swap(0, this.size() - 1) // 将根和最后一个元素交换
		this.heap.pop() // 防止对象游离
		this.#sink(0) // 下沉，恢复有序性
		return max
	}
	// 第i个是否小于第j个
	#defaultCompare(a, b) {
			return a < b
	}
	// 交换
	#swap(i, j) {
		[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]]
	}
	// 上浮
	#swim(k) {
		let parent = this.#getParentIndex(k)
		while(k > 0 && this.compare(this.heap[parent], this.heap[k])) {
			this.#swap(parent, k)
			k = parent
			parent = this.#getParentIndex(k)
		}
	}
	// 下沉
	#sink(k) {
		while (this.#getLeft(k) < this.size()) {
			let j = this.#getLeft(k)
			// j 指向子节点的较大值
			if (j+1 < this.size() && this.compare(this.heap[j], this.heap[j+1])) j++
			// 如果子节点都小
			if (this.compare(this.heap[j], this.heap[k])) break
			this.#swap(k, j)
			k = j
		}
	}
}

测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
const mh = new Heap((a,b)=>a.val<b.val)
mh.insert({val: 20})
mh.insert({val: 45})
mh.insert({val: 56})
mh.insert({val: 12})
mh.insert({val: 93})
mh.insert({val: 34})
mh.insert({val: 12})
mh.insert({val: 84})
console.log(mh.heap)
// [
//   { val: 93 },
//   { val: 84 },
//   { val: 45 },
//   { val: 56 },
//   { val: 20 },
//   { val: 34 },
//   { val: 12 },
//   { val: 12 }
// ]
mh.delete()
mh.delete()
console.log(mh.heap)
// [
//   { val: 56 },
//   { val: 20 },
//   { val: 45 },
//   { val: 12 },
//   { val: 12 },
//   { val: 34 }
// ]

堆排序

（1）先原地创建一个最大堆，因为叶子节点没有子节点，因此只需要对非叶子节点从右向左进行下沉操作

（2）把堆首（堆的最大值）和堆尾替换位置，堆大小减一，保持非堆是递增的，保持数组最后一个元素是最大的，最后对堆首进行下沉操作（或者说把非堆重新堆化）。

（3）重复第二步直至清空堆。

注意：排序的数组第一个元素下标是 0 ，跟上面处理边界不一样。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
function heapSort (arr) {
	// arr = arr.slice(0) // 是否原地排序
	let N = arr.length - 1
	if (!arr instanceof Array) {
		return null
	}else if (arr instanceof Array && (N === 0 || N === -1) ) {
		return arr
	}
	function exch(i, j) {
		[arr[i], arr[j]] = [arr[j], arr[i]]
	}
	function less(i, j) {
		return arr[i] < arr[j]
	}
	function sink(k) {
		while (2 *k + 1 <= N) {
			let j = 2 * k + 1
			// j 指向子节点的较大值
			if (j+1 <= N && less(j, j+1)) {
				j++
			}
			// 如果子节点都小
			if (less(j, k)) break
			exch(k, j)
			k = j
		}
	}
	// 构建堆
	for(let i = Math.floor(N/2); i >= 0; i--) {
		sink(i)
	}
	// 堆有序
	while (N > 0) {
		exch(0, N--)
		sink(0)
	}
}

另一个实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
function heapSort (arr) {
	// arr = arr.slice(0) // 是否原地排序
	let N = arr.length
	if (!arr instanceof Array) {
		return null
	}else if (arr instanceof Array && (N === 0 || N === -1) ) {
		return arr
	}
	function getParentIndex(idx) {
		return Math.floor((idx-1)/2)
	}
	function getLeft(idx) {
		return idx * 2 + 1
	}
	function getRight(idx) {
		return idx * 2 + 2
	}
	function swap(i, j) {
		[arr[i], arr[j]] = [arr[j], arr[i]]
	}
	function compare(i, j) {
		return i < j
	}
	function sink(k) {
		while (getLeft(k) < N) {
			let j = getLeft(k)
			// j 指向子节点的较大值
			if (j+1 < N && compare(arr[j], arr[j+1])) j++
			// 如果子节点都小
			if (compare(arr[j], arr[k])) break
			swap(k, j)
			k = j
		}
	}
	// 构建堆
	for(let i = Math.floor(N/2); i >= 0; i--) {
		sink(i)
	}
	// 堆有序
	while (N > 1) {
		swap(0, --N)
		sink(0)
	}
}

测试

1
2
3
4
5
6
7
8
const arr1 = [15, 20, 30, 35, 20, 50, 40, 80, 10, 40, 90]
heapSort(arr1)
console.log(arr1)
// [10, 15, 20, 20, 30, 35, 40, 40, 50, 80, 90]
const arr2 = [62, 88, 58, 47, 35, 73, 51, 99, 37, 93];
heapSort(arr2)
console.log(arr2)
// [35, 37, 47, 51, 58, 62, 73, 88, 93, 99]

参考

  1. algs4
  2. 【JS手写最小堆（小顶堆）、最大堆（大顶堆）】：https://juejin.cn/post/7128369000001568798
  3. 【数据结构与算法(4)——优先队列和堆】：https://zhuanlan.zhihu.com/p/39615266
  4. 【最大堆最小堆及堆排序】：https://mingshan.fun/2019/05/14/heap/
  5. 【搞定JavaScript算法系列–堆排序】：https://juejin.cn/post/6844903830258188296